LINE SHAFT PULLEYS and BELTINGBrought to you by Harry's Old Engine...Everything you've ever wanted to know about a lineshaft and then some...  Click for color photo. Kinematics of Flexible Gearing1. Transmission by Belts, Ropes, and Chains. The transmission of motion and power between shafts that are some distance apart may be effected by belts, ropes, or chains running over suitable pulleys. Belts form a convenient means of transmitting power, but owing to their tendency to stretch and slip on the pulleys, they are not suitable where an exact velocity ratio between the shafts is required. For driving machinery, however, this freedom to stretch and slip is an advantage, since it prevents shocks that are liable to occur when a machine is thrown suddenly into gear, or when there is a sudden fluctuation in the load. For transmitting considerable power between shafts at some distance apart, ropes are frequently used instead of belts. The advantages of rope driving are lightness, low first cost, smooth running, flexibility, and case of repair. With rope drives, the shafts connected are generally run at high speeds. Chain gearing is used when positive driving is essential, and also for the transmission of large powers. Ordinarily, with chain drives the motion is slow, although recently chains of special forms have been devised for highspeed transmission, and these are being used quite extensively in place of belts. VELOCITY RATIO IN BELT AND ROPE DRIVES2. Velocity Ratio of a Pair of Pulleys. Let the pulleys a and b Fig. 1, be connected by a belt or rope, and let Da and Db denote their respective diameters, and Na and Nb their respective velocities, expressed in revolutions per minute. The speed of a point on the circumference of either pulley, assuming that the belt neither slips nor stretches, is the same as the speed of the belt. 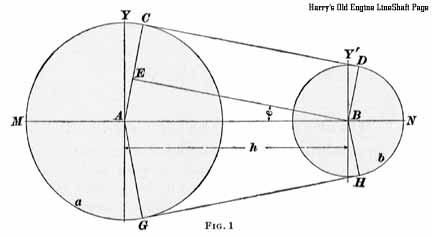 Then v, the speed of the belt, in feet per minute, is equal to the product of the circumference of the pulley, in feet, and the revolutions per minute. That is, v = pi Da Na and v = pi Db Nb; hence, pi Da Na = pi Db Nb and(1) Da Na=Db Nb or (2) Na/Nb = Db/Da That is, the speeds or numbers of revolutions of two pulleys connected by belt are inversely proportional to their diameters. In formulas 1 and 2, the diameters may be taken in either feet or inches, but the same unit must in every case be used for both diameters. EXAMPLE 1. A pulley 30 inches in diameter, making 210 revolutions per minute, drives a second pulley 14 inches in diameter; how many revolutions per minute does the latter pulley make? SOLUTION. From formula 1, 30 x 210 = 14 x Nb; whence Nb = 30 x 210 / 14 = 450 R. P. M. Ans. EXAMPLE 2. The driving pulley of a machine is 1 foot in diameter and must make 750 revolutions in 5 minutes; what size pulley should be used on the driving shaft, if its speed is 143 revolutions per minute? SOLUTION. In all examples of this kind, the speeds and diameters must be reduced to the same units. 750 revolutions in 5 minutes = 750 / 5 = 150 R. P. M.; 1 ft. = 12 in. Hence, 12 X 150 = Db X 143, whence Db = 12 X 150 / 143 = 12.6 in., nearly. Ans. 3. Influence of Belt Thickness. The formulas in Art. 2 are based on the assumption that the thickness of the belt is so small in comparison with the pulley diameter that it can be neglected. Actually, only the center line of the belt or rope has a constant speed v; hence, if t denotes the thickness of belt or rope, the effective radii are ra + 1/2 t and rb + 1/2 t, while the effective diameters are Da + t and Db + t, respectively. Formula 1, Art. 2, therefore becomes (1) Na (Da + t) = Nb (Db + t)and formula 2, Art. 2, becomes (2) Na/Nb = Db + t / Da + t EXAMPLE. If, in the first example of Art. 2, the belt thickness is 3/8 inch, how many revolutions per minute does the 14 inch pulley make, taking account of this thickness? SOLUTION. From formula 1, Na (Da + t) = Nb (Db +t), whence,210 X (30 + 3/8) = Nb X (14 + 3/8) and Nb = 210 X (30 3/8 / 14 3/8) = 444 R. P. M., nearly. Ans. Hence, by taking belt thickness into account, the speed of the driven pulley is reduced from 450 to 444 revolutions per minute, or about 1.3 percent. In practice, however, the thickness of the belt is usually neglected. 4. Velocity Ratio In Compound System of Belts. In Fig. 2 is shown a compound system of belts in which there are six pulleys, a, b, c, d, e, and f. Denoting the diameters by Da Db, etc. and the revolutions per minute by Na, Nb, etc., for the three pair a and b, c and d, a and f, the following relations exist: Na / Nb = Db / Da, Nc / Nd = Dd / Dc, and Ne / Nf = Df / De. Multiplying together the left-hand and right-hand members, respectively, of these three equations, and placing the products
equal to each other, Na X Nc X Ne / Nb X Nd X Nf = Db X Dd X Df / Da X Dc X De. Now, pulleys b and c are fixed to the same shaft and make the same number of revolutions per minute; hence, Considering separately the three pair connected by the three belts, pullevs a, c, and e may be taken as the drivers, 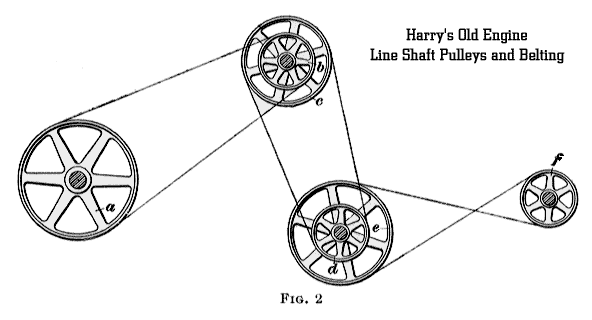 R. P. M. of first driver / R. P. M. of last follower = Product of diameters of all followers / Product of diameters of all drivers; and formula 2 thus: The speed of the first driver multiplied by the product of the diameters of all the drivers is equal to the speed of the last follower multiplied by the product of the diameters of all the followers. The thickness of the belt may be taken into account by increasing all pulley diameters by an amount equal to that thickness. EXAMPLE. An emery grinder Is to be set up to run at 1,200 revolutions per minute. The countershaft has pulleys 20
and 8 inches in diameter. The pulley on the grinder is 6 inches In diameter and is belted to the 20-inch pulley on the
countershaft. The line shaft runs at 180 revolutions per minute and carries a pulley that is belted to the 8-inch pulley
on the countershaft. Calculate the diameter of tile line shaft pulley. SOLUTION. From formula (2), 180 X D X 20 = 1,200 X 8 X 6, whence D = (1,200 X 8 X 6) / (180 X 20) = 16 in. Ans. 5. Pulley Diameters. When the speeds of the first and last shafts are given, and the diameters of all the pulleys are to be found, the following rule may be applied: Rule. Divide the higher speed by the lower. If two Pulleys are to be used, this quotient will be the ratio of their diameters. If four pulleys are required, find two numbers whose product is equal to this quotient. One of these numbers will
be the ratio of the diameters of one pair of pulleys, and the other number will be the ratio for the other pair. EXAMPLE. It is required to run a machine at 1,600 revolutions per minute, the driving shaft making 320 revolutions
per minute; what size pulleys are required: (a) when two pulleys are used; (b) when four pulleys are used? SOLUTION. (a) 1,600 / 320 = 5. The two pulleys must, therefore, be in the ratio of 5 to 1, the driving pulley being five
times as large as the driven pulley, since the latter has the greater speed. Then assume diameters of 30 and 6 in. Ans. 6. Direction of Rotation. When a belt connecting two pulleys forms a single loop, it is called an open belt. If, however, it forms. a double loop, like a figure 8, it is called a crossed belt. Thus, in Fig. 2, the pulleys a and b are connected by an open belt,
as are the pulleys c and d, while a crossed belt connects the pulleys e and f. Pulleys connected by open belts turn in the same direction, and those connected by crossed bells in opposite directions. If several belts are used between the first driver and last follower, these will turn in the same direction if there is no crossed belt, or if there is an even number of crossed belts, but in opposite directions If the number of crossed belts is odd. EXAMPLES FOR PRACTICE1. A driving pulley is 54 inches in diameter, and the driven pulley, which runs at 112 revolutions per minute,
is 2 1/2 feet in diameter; what is the speed of the driving shaft? 2. The flywheel of an engine running at 180 revolutions per minute is 8 feet 5 inches in diameter; what should
be the diameter of the pulley that it drives if the required speed of the latter is 600 revolutions per minute? 3. A machine is to be belted through a countershaft, so as to run at 1,200 revolutions per minute, the speed of
the driving shaft being 120 revolutions per minute; find three ratios that could be used for two pair of pulleys. 4. An emery grinder is to be set to run at 1,400 revolutions per minute; the countershaft has pulleys 30 and 8 inches
in diameter; the pulley on the grinder is 7 inches in diameter; what size pulley should be used on the line shaft, its
speed being 185 revolutions per minute? LENGTHS OF OPEN AND CROSSED BELTS7. Length of an Open Belt. In the discussion of the lengths of belts the following symbols will be used: In Fig. 1, M C D N represents half the length of the belt. This distance is made up of three parts,
M C, CD, and DN, so that In the figure, the radii A C and B D are drawn perpendicular to the common
tangent CD, and hence they are parallel. Furthermore, B E is drawn parallel to D C,
and B E C D is therefore a rectangle. Hence, B E is equal to C D and makes
the same angle e with M N as would C D if it were extended to meet M N.
Also, C E = D B = r. But, A E = A C - CE, and since,
A C = R and C E = r, A E = R - r. Now, the angles Y A C
and Y' B D have their sides respectively perpendicular to the sides of the angle e. Hence, by
geometry, angle Y A C = angle Y' B D = angle e. And since the angles M A Y
and Y' B N are right angles, it follows that the angle M A C = 90 degrees + e,
and the angle D B N = 90 degrees - e. The circumference of the larger pulley is 2 pi R, and the arc M C bears the same ratio to the whole circumference that the angle M A C bears to 360 degrees. In other words, M C : 2 pi R =
90 + e : 360, or the arc M C = 2 pi R X (90 + e )/ 360 = pi R X (90 + e)/180. Substituting these values of M C, C D, and D N in formula 1, Since A E / A B = R - r / h = d / h = sin e, the angle e may readily be found from a table of natural sines by taking the angle corresponding to the value that equals d/h. This value of e, in degrees, is substituted in formula 2. EXAMPLE. In Fig. 1, let the pulleys have diameters of 20 and 12 inches, respectively, and let the distance between the centers
of the shafts be 4 feet; calculate the length of the open belt required. SOLUTION. R = 10, r = 6, d = 10 - 6 = 4, s = 10 + 6 = 16, and h = 48 in. 8.When the angle e is comparatively small, the followIng formula gives a sufficiently exact approximation to
the length of an open belt: The greater the difference in radii and the smaller the distance between the pulleys, the less exact is the formula. EXAMPLE. Solve the example of Art. 7 by the approximate method. 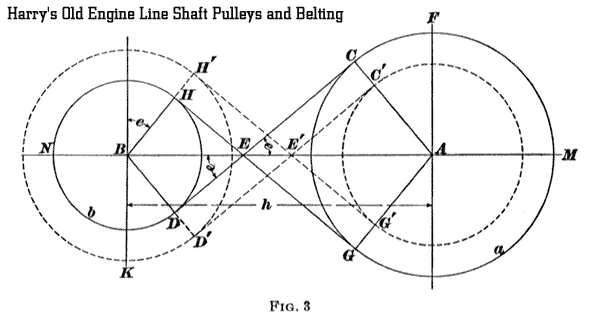 9. Length of a Crossed Belt. Referring to Fig. 3, it appears that for the half length of the crossed belt The angles C E A and D E B are each equal to e, and the radii A C
and B D are drawn perpendicular to C D. Hence, the angles C A F and D B K
are each equal to e, since their sides are perpendicular, respectively, to the sides of C E A and D E B. The angle e may be determined from the triangles A C E and B D E, in which EXAMPLE. In the example of Art. 7, calculate the length of the belt if it is a crossed belt. SOLUTION. R - 10; r = 6; d = 10 - 6=4; s =10 + 6 = 16; and h = 48. By formula 4, EXAMPLES FOR PRACTICE1. Two pulleys have diameters of 36 inches and 20 inches, respectively, and the distance between their centers is
128 Inches; find the length of an open belt to connect them. Ans. 344.5 in. 2. What length of crossed belt is required to connect two pulleys of 42 inches and 18 inches diameter, respectively, if the distance
between shaft centers is 8 feet? Ans. 295.7 in. 3. Using the formula of Art. 8, find the length of an open belt to connect two pulleys 30 inches and 36 inches in diameter,
respectively, the distance between centers being 12 feet. Ans. 391.7 In. CONE PULLEYS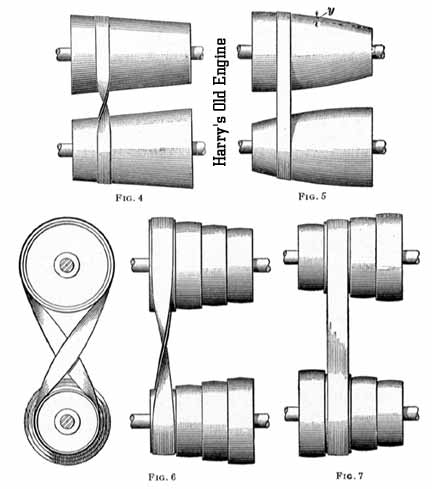 10. Variable Speed. Speed cones are used for varying the speed of a shaft or other rotating piece driven by a belt.
Figs. 4 and 5, respectively, show continuous cones and conoids, the former being suitable for crossed and the latter for open belts.
The speed of the driven shaft can be raised gradually by shifting the belt. Figs. 6 and 7 show sets of stepped pulleys. As a flat
belt always tends to run to the larger end of a conical pulley, continuous cones or conoids require special provision for keeping
the belt at any desired point on the pulley. For this reason, stepped cones, rather than continuous cones, are generally used.
Whenever possible, it is desirable to have both pulleys alike, so that they can be cast from one pattern. 11. Continuous Cones for Crossed Belts.
Since a and b are to be the same size, a certain relation must exist between N and n1 and n2. From formula 1, Art. 2, N D = n, d, or D = n1 d / N, and That is, N must equal the square root of the product of n1 and n2. Having determined N, the relation between D and d can be found. Since N = (n1 d)/D and N = (n2 D)/d, (n1 d)/d = (n2 D)/d or n1 d X d = n2 D X D Hence, EXAMPLE. Two continuous speed cones are to be designed to give a range of speed between 100 and 700 revolutions per minute; they are to be alike in all respects. What must be the speed of the driving shaft and the large diameter of the cones, assuming the small diameter to be 4 inches? SOLUTION. From formula 1, 12. Cone Pulleys for Crossed Belts.Speed cones, to be properly designed, should have their diameters at different points so proportioned that the belt will always have the same length, when tightly drawn, whatever its position. With crossed belts, this condition is easily fulfilled, as it is only necessary to make the sum of the corresponding diameters or radii the same for all pairs of steps, or, in the case of the continuous cones, for all belt positions. The truth of this statement may be shown as follows: In Fig. 3, suppose the belt to run on the pulleys shown by dotted lines, the sum of whose radii is equal to the sum of the radii of the pulleys a and b. Then, since it is assumed that A G + B H = A G' + B H', it f ollows, by subtracting A G' + B H from both members of the equation, that A G - A G' = B H' - B H, or G G' = H H', and it can be proved by geometry that G' H' is parallel to G H and equal to it in length. Likewise C' D' is equal to and parallel to C D. Then the right triangles C E A and C' E' A have the angle C A E in common. Also, the angles A C E and A C' E' are equal, since each is a right angle. Now, the sum of the three angles of a triangle is equal to two right angles, and since the triangles C E A and C' E' A have two angles of the one equal to two angles of the other, it follows that their third angles are equal, or C E A = C' E' A. Theref ore, with the belt in the position shown by the dotted lines, the sum s, the angle e, and the distance h are the same as for the position shown by full lines. Consequently, the length of belt as found by formula 3, Art. 9, will be the same in both cases. Hence, for crossed bells, the sum of the corresponding diameters of two speed cones should be the same at all points. EXAMPLE. The steps of a cone pulley have diameters of 7, 8 3/8, 10, and 12 inches, respectively, and the diameter of the step on the other cone corresponding to the 10-inch step is 8 3/4 inches; calculate the diameters of the remaining steps for a crossed belt. SOLUTION. SUM of diameters = 10 + 8 3/4 = 18 3/4 In. Since this Is to be the same for all pairs, the diameters of the remaining steps are as follows: 13. Cone Pulleys for Open Belts. When an open belt is used, the sum of the diameters does not remain the same. In order that the belt shall run equally tight in all positions or on all steps, the sum of the corresponding diameters D + d is the smallest when D - d has its greatest value, that is, when the diameters are most unequal, and is greatest when D = d, that is, when the diameters are equal. The difference between cones for, open and for crossed belts is shown in Figs. 4 and 5. With the crossed belt, the sides of the cone are straight, while with the open belt the sides bulge near the middle sections, showing that the sum D + d is greater at the center than at the ends. The distance y, Fig. 5, must be added to each radius at the middle section to make the cones of Fig. 4 suitable for an open belt. 14. Numerous formulas are given for finding corresponding step diameters, but they are approximate, and are, moreover, not easy to apply. The following graphic method is very accurate, is easy to use, and is generally considered preferable to methods making use of calculations. It is known as Burmester's method. Let A Z, Fig. 9, be a horizontal line, and A W a line at 45 degrees with A Z. From A, lay off A B on A W to represent to some scale the distance h between the axes of the cones. From B, lay off B C at right angles to A B and make B C = 1/2 A B. Then, with A C as a radius and A as a center, draw the arc C D E. Now, draw any line X X parallel to A Z and cutting A B at 0. Locate on the arc C D E any points, 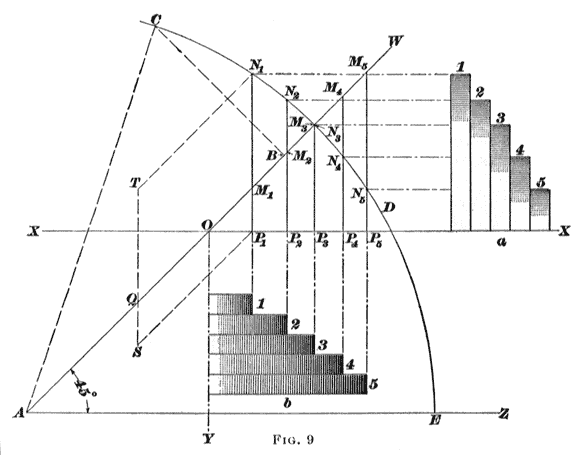 If 0 X be taken as the axis of one stepped cone, the steps may be found by projecting horizontally from N1, N2, etc. The half cone thus obtained is shown at a. The other cone b may be laid off on the vertical line 0 Y as an axis by projecting vertically from the points P1, P2 P3, etc. The corresponding steps on a and b have the same numbers; thus 2 goes with 2, 3 with 3, and so on. The actual sizes of the cones depend on the location of the axis X X. If this line is raised so that 0 is nearer B, the radii of all steps on both cones will be smaller; and conversely, if 0 is taken nearer A, all radii will be greater. Usually the radii of one pair of steps are given or assumed, and in this case the axis X X can be located as follows: Take any point Q on A B and lay off Q S vertically downwards to represent the smaller radius r; then from the point S lay off S T upwards to represent the larger radius R. These radii are drawn to the same scale as A B is drawn to represent h. Now through S and T draw lines parallel to A B, and through N1, where the line from T cuts the arc C D E, draw a vertical line cutting the line from S in P1; then through P1, draw the axis X X cutting A W in 0. 15. Frequently, the steps of cones are to be given diameters such that definite velocity ratios, fixed beforehand, will be given as the belt is shifted to different pairs of steps. An example will show how this may be done. Suppose that each cone is to have five steps; that the cones are to be alike, so that they may be cast from the same pattern; and that the velocity ratios for the first two pair are 4 and 2, respectively. The distance h is known or assumed. Let it be 40 inches. Since the cones are to be alike and the number of steps is odd, the diameters of the middle steps must be the same; let this diameter be taken as 16 inches. For an open belt, the other steps are found by the following method: In Fig. 10, make A B = 40 inches to some scale, and draw the arc C D E as described in connection with Fig. 9. From the intersection D drop a vertical line; on this lay off D P3 equal to the radius of the middle step, or 16/2 inches, to the same scale as A B, and through P3 draw the axis X X. On X X lay off, from 0, any convenient length 0 H, erect a vertical line at H, and then lay off H K = 1/4 OH and HL = 1/4 OH. Join K and L to O, and let N1, and N2 represent the intersections of the lines, 0 K and 0 L with the arc C D E. Then from N1 and N2 drop the perpendiculars N1 P1 and N2 P2 on O X. Now O P1 and P1 N1 are the first pair of radii, and OP2 and P2 N2 the second pair. These pairs give the required velocity ratios 4 and 2; for, since the triangles O P1 N1 and O H K are similar, the ratio of the radii R1 : r1 = 0 P1 : P1 N1 = 0 H: H K = 4: 1; and since the triangles 0 P2 N2 and 0 H L are similar, R2 : r2 = 0 P2 : P2 N2 = O H: H L = 2: 1. 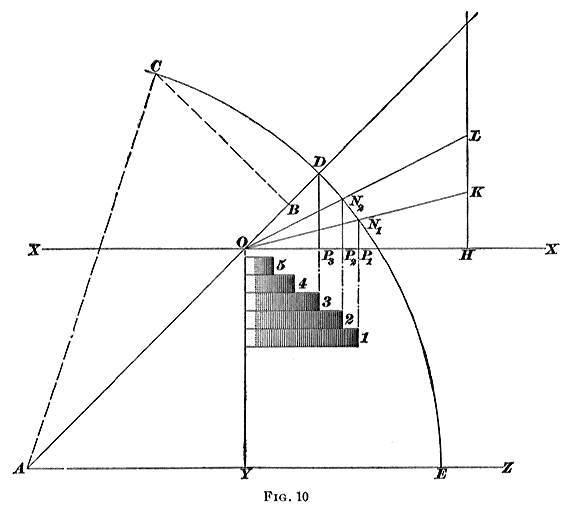 The lines 0 P3 and P3 D, which are equal, give the radii R3 and r3 of the middle steps. Projecting P1, P2, and P3 parallel to 0 Y, the steps 1, 2, and 3 of the cone b are obtained. Now, since the cones are to be alike, step 4 of cone b must have the same radius as step 2 of cone a, that is, P2 N2; and step 5 of b must have the radius P1 N1 of step 1 of cone a. By measurement, the various radii are as follows:
For a crossed belt; the problem is easily solved by a simple calculation. The sum of the radii of the equal middle steps is R3 + r3 = 8 + 8 = 16 inches, and this sum is constant. That is, R1 + r1 = 16. But R1 = 4 r1 for this pair of pulleys. Then 4 r1 + r, = 16, 5 r1 = 16, or r1 = 3.2 inches, and R1 = 16 - 3.2 = 12.8 inches. Also, R2 + r2 = 16. But R2 = 2 r2 for this pair. Hence, 2 r2 + r2 = 16, 3 r2 = 16, or r2 = 5.33 inches, and R2 = 16 - 5.33 = 10.67 inches. If the distance between, the axes of the pulleys to be connected by open belt is great, or if, as is sometimes the case, one of the axes is adjustable, the diameters can be calculated as though the belt were crossed. Otherwise, when designed for open belts, they should be laid out as described in Arts. 14 and 15. EXAMPLES FOR PRACTICE1. Two continuous speed cones are required to give a range of speed between 100 and 600 revolutions per minute; assuming the large diameters of the cones to be 14 inches, what must be: (a) the small diameters; and (b) the speed of the driving shaft? Both cones are to be alike. Ans. (a) 5.71 in. (b) 244.95 R. P. M. 2. In example 1, if the speed of the driving shaft were 260 revolutions per minute, and the slowest speed of the driven cone 140 revolutions: (a) what would be the greatest speed of the driven cone? (b) what would be the ratio of the large and small diameters of the cones? Ans. a) 482.86 R. P. M. (b) 1. 86 : 1 3.The radii of one of two speed cones are 3, 5 1/2, 8, and 10 inches and the radius of the step on the second cone corresponding to the 8-inch step on the first cone is 6 inches. Find the radii of the second cone, the distance between shafts being 30 inches and an open belt being used. Ans. 10 7/16, 8 1/16, 6, and 3 5/8 in. 4. The distance between the axes of two cones is 36 inches and an open belt is used. The two cones are to be alike, and are required to give velocity ratios as follows: The radii of the first pair are, respectively, 15 Inches and 5 inches. Find, by the graphic method, the radii of the other pairs.
5. With the data of example 4, calculate the radii for a pair of cones with a crossed belt. Ans. POWER TRANSMISSION BY BELT |
Reprinted by Harry Matthews © 2001, 2005. ALL RIGHTS RESERVED!
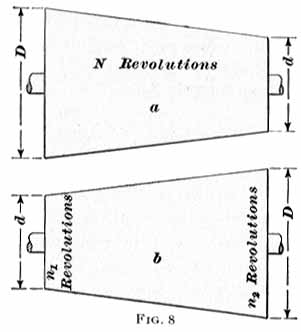 Let a and b, Fig. 8, represent two speed cones of the same size, having the diameters of the large and small ends equal to D and d, respectively. The driving cone a has a uniform speed of N revolutions per minute, while the speed of b is n1 or n2 revolutions per minute, according as the belt runs at the small or large end. It is assumed that pulley b is to have a range of speeds between n1 and n2 revolutions, n1 being the greater.
Let a and b, Fig. 8, represent two speed cones of the same size, having the diameters of the large and small ends equal to D and d, respectively. The driving cone a has a uniform speed of N revolutions per minute, while the speed of b is n1 or n2 revolutions per minute, according as the belt runs at the small or large end. It is assumed that pulley b is to have a range of speeds between n1 and n2 revolutions, n1 being the greater.